Explorando las propiedades sorprendentes de la onda sinusoidal

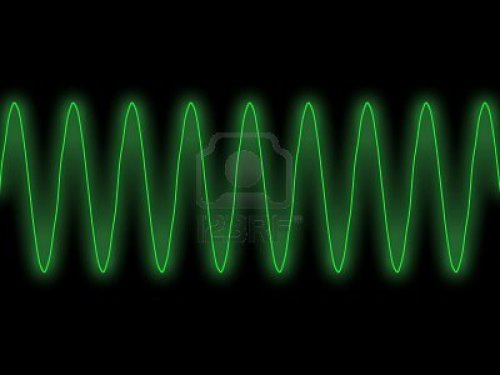
Si estás buscando una explicación completa sobre las ondas sinusoidales, has llegado al lugar correcto. En este artículo, nuestro equipo te brindará una guía detallada sobre este fenómeno fundamental en ciencias y tecnología. Conocerás los conceptos básicos, las propiedades y características, así como las aplicaciones más comunes de las ondas sinusoidales.

¿Qué es una onda sinusoidal?

Una onda sinusoidal es un tipo de onda periódica que se caracteriza por tener una forma de ondulación suave y continua, representada por una función matemática llamada seno (sin). Se utiliza para describir fenómenos naturales y artificiales que siguen este patrón, como el sonido, la luz y las señales eléctricas.

Importancia de las ondas sinusoidales en las ciencias y la tecnología

Las ondas sinusoidales son fundamentales en diversas disciplinas científicas y tecnológicas debido a su comportamiento predecible y su capacidad para transmitir información de manera eficiente. Estas ondas se encuentran presentes en la física, las matemáticas, la ingeniería y la música, entre otras áreas. Comprender sus propiedades y características es esencial para el desarrollo de tecnologías y la explicación de fenómenos naturales.

Conceptos básicos sobre las ondas sinusoidales

Amplitud y frecuencia de una onda sinusoidal

La amplitud de una onda sinusoidal es la máxima distancia alcanzada por una partícula vibrante desde su posición de equilibrio. Representa la altura del pico y del valle de la onda. Por otro lado, la frecuencia de una onda sinusoidal indica la cantidad de ciclos completos que la onda realiza en un segundo. Se mide en hercios (Hz) y está relacionada con el tono de un sonido o la capacidad de transmitir información en el caso de las señales eléctricas.

Periodo y fase de una onda sinusoidal

El periodo de una onda sinusoidal es el tiempo que tarda en completar un ciclo. Se mide en segundos y es inversamente proporcional a la frecuencia. Es decir, a mayor frecuencia, menor periodo, ya que la onda se repite con mayor rapidez. La fase de una onda sinusoidal indica la posición relativa de la onda en un instante específico. Se representa en grados o radianes y determina el desplazamiento horizontal de la onda.

Propiedades y características de las ondas sinusoidales

Simetría y periodicidad

Las ondas sinusoidales son simétricas en relación a su eje central, lo que significa que su forma se repite de manera idéntica en ambos lados del eje. Esta simetría contribuye a su periodicidad, es decir, a su capacidad de repetirse a intervalos regulares.

Desplazamiento vertical

El desplazamiento vertical de una onda sinusoidal se refiere a su posición en relación con un valor de referencia. Puede tener un valor positivo, negativo o ser nulo, lo que determina si la onda se encuentra por encima o por debajo de la línea de equilibrio.

Amplitud y frecuencia angular

La amplitud de una onda sinusoidal, como se mencionó anteriormente, es la máxima distancia alcanzada por una partícula vibrante. La frecuencia angular, por otro lado, se calcula multiplicando la frecuencia por 2π y se representa como ω (omega). La frecuencia angular está relacionada con el período de la onda y se utiliza en cálculos matemáticos y físicos más avanzados.

Fase y desfase

La fase de una onda sinusoidal indica la posición relativa de la onda en un instante específico, mientras que el desfase se refiere al desplazamiento horizontal de la onda en relación con otra onda de referencia. El desfase se mide en grados o radianes y puede tener un valor positivo o negativo.

Velocidad de propagación

La velocidad de propagación de una onda sinusoidal indica la velocidad a la que se desplaza a través de un medio. Este valor depende de las características del medio y se representa por la letra v. En general, las ondas sinusoidales se propagan a una velocidad constante en un medio homogéneo.

Términos relacionados con las ondas sinusoidales

Amplitud máxima y mínima

La amplitud máxima se refiere al valor máximo positivo alcanzado por la onda sinusoidal, mientras que la amplitud mínima es el valor máximo negativo. Estos valores determinan la diferencia extrema entre el pico y el valle de la onda.

¡Descubre qué es la velocidad de escape y cómo alcanzarla a toda costa!

Pico y valle

El pico de una onda sinusoidal es el valor máximo positivo alcanzado, mientras que el valle es el valor máximo negativo. Estos puntos representan los extremos de la onda.

Longitud de onda

La longitud de onda representa la distancia física entre dos puntos correspondientes de la onda sinusoidal, como dos picos o dos valles consecutivos. Se simboliza por la letra griega λ (lambda) y se mide en metros.

Frecuencia y período

La frecuencia de una onda sinusoidal indica la cantidad de ciclos completos que la onda realiza en un segundo. El período, por otro lado, es el tiempo que tarda en completar un ciclo. Ambos términos están relacionados de manera inversa: a mayor frecuencia, menor período.

Aplicaciones de las ondas sinusoidales

Comunicaciones inalámbricas

Las ondas sinusoidales son ampliamente utilizadas en las comunicaciones inalámbricas, como la transmisión de señales de radio y televisión. La amplitud y frecuencia de las ondas son moduladas para llevar información a través del espacio y permitir la comunicación a largas distancias.

Música y sonido

En el ámbito musical, las ondas sinusoidales son esenciales para la generación de sonidos. Cada nota musical puede representarse como una onda sinusoidal con una frecuencia y amplitud específicas. La reproducción de sonido también se basa en la combinación de diferentes ondas sinusoidales para crear una representación fiel de los sonidos reales.

Electrónica y circuitos

En la electrónica y los circuitos, las ondas sinusoidales son utilizadas para la generación y modulación de señales. Por ejemplo, en la generación de corriente alterna, donde las ondas sinusoidales son la base de la transmisión de energía eléctrica a través de la red.

Conclusión

Las ondas sinusoidales son un fenómeno fundamental en las ciencias y la tecnología, con numerosas aplicaciones en nuestra vida cotidiana. Comprender sus propiedades y características nos permite estudiar fenómenos naturales, desarrollar tecnologías y disfrutar de la música. Esperamos que esta guía haya sido útil para comprender mejor estos conceptos y su importancia en nuestro mundo.

Preguntas frecuentes

¿Cómo se relaciona la frecuencia con la longitud de onda?

La frecuencia y la longitud de onda están inversamente relacionadas. A medida que la frecuencia aumenta, la longitud de onda disminuye, ya que un mayor número de ciclos se completa en un período de tiempo dado. Podemos utilizar la fórmula λ = v/f, donde λ es la longitud de onda, v es la velocidad de propagación y f es la frecuencia.

¿Cuál es la diferencia entre amplitud y frecuencia de una onda sinusoidal?

La amplitud de una onda sinusoidal se refiere a la máxima distancia alcanzada por la onda, es decir, la diferencia entre el pico y el valle. Mientras tanto, la frecuencia indica la cantidad de ciclos completos que la onda realiza en un segundo. La amplitud determina la intensidad de la onda, mientras que la frecuencia está relacionada con el tono o la capacidad de transmitir información.

¿Cuál es la importancia de las ondas sinusoidales en la transmisión de señales?

Las ondas sinusoidales son fundamentales en la transmisión de señales debido a su comportamiento predecible y su capacidad para llevar información. La modulación de la amplitud y frecuencia de las ondas sinusoidales permite la transmisión de sonidos, imágenes y datos a través del espacio y el cableado. Esta propiedad ha revolucionado las comunicaciones y ha permitido el desarrollo de tecnologías como la telefonía móvil, la televisión y las redes inalámbricas.

¿Se pueden representar las ondas sinusoidales de otras formas además de la gráfica?

Sí, además de la representación gráfica, las ondas sinusoidales pueden describirse mediante ecuaciones matemáticas y representaciones complejas. Existen diversas formas de representar una onda sinusoidal, como la representación polar, la forma rectangular y la descomposición en series de Fourier. Estas representaciones permiten realizar cálculos y modelar fenómenos con mayor precisión.

Descubre el poder oculto de los materiales paramagnéticos y diamagnéticos